跳转到主要内容

Python `itertools.permutations` 使用的排列算法

发布于 长文 4436 字 9 分钟
似乎之前没人写过？那就我来吧。

TL;DR：这本质上是一个基于回溯，利用元素交换的递归排列生成算法，但被重写成了循环形式（可能出于效率考量）。

引子

最近在算法复健，刷到了排列相关的题目。恰巧 Python 内置了一个非常实用的工具库 itertools，其中有一个 permutations(iterable, r) 方法，可以对一个给定的 iterable 生成所有大小为 r 的排列，且输出按照字典序排列。

>>> list(permutations('ABCD', 2))
[('A', 'B'), ('A', 'C'), ('A', 'D'), 
 ('B', 'A'), ('B', 'C'), ('B', 'D'), 
 ('C', 'A'), ('C', 'B'), ('C', 'D'), 
 ('D', 'A'), ('D', 'B'), ('D', 'C')]

在我之前所接触的算法中，排列生成要么是基于回溯，要么是基于字典序，但无论哪种都只能生成全排列，而无法生成这样的部分排列（指生成的排列长度 r 和原输入长度 n 不同）。另一条思路是先生成所有长度为 r 的组合，然后再在每个组合内生成全排列，但这样无法保证输出按字典序（除非先手动收集再排序）。

于是我打开了 Python 的 itertools 的官方文档，其中提供了与 CPython 实现等价的 Python 代码，permutations 方法的代码如下（🔗）：

def permutations(iterable, r=None):
    # permutations('ABCD', 2) --> AB AC AD BA BC BD CA CB CD DA DB DC
    # permutations(range(3)) --> 012 021 102 120 201 210
    pool = tuple(iterable)
    n = len(pool)
    r = n if r is None else r
    if r > n:
        return
    indices = list(range(n))
    cycles = list(range(n, n-r, -1))
    yield tuple(pool[i] for i in indices[:r])
    while n:
        for i in reversed(range(r)):
            cycles[i] -= 1
            if cycles[i] == 0:
                indices[i:] = indices[i+1:] + indices[i:i+1]
                cycles[i] = n - i
            else:
                j = cycles[i]
                indices[i], indices[-j] = indices[-j], indices[i]
                yield tuple(pool[i] for i in indices[:r])
                break
        else:
            return

尝试初步理解

虽然顶部有两行注释，不过这也只是描述了这个方法的效果，对其原理并没有任何解释。往后继续看，可以发现算法首先构造了两个 list：indices 和 cycles，且之后每次输出结果（yield）实际上都是将 indices 中的前 r 个输出。再往后算法进入了一个神秘的 for 循环，对 cycles 中的元素做了一些修改，用 cycles 的值对 indices 中的一些元素做了交换。仅从代码层面出发，对算法的理解似乎也就止步于此了。然而这并没有回答一个重要问题：为什么这个算法能工作？

寻找相关信息

考虑到 itertools 库是在 Python 2.3 （2003 年 7 月）被引入标准库的，这个算法已经算得上历史悠久了。再加之 itertools 库的广泛使用，这个算法的原理应该是早已被详尽记录的。带着这样的期望，我开始用各种关键词组合搜索相关信息。可惜的是，除了 Stack Overflow 上一个 2010 年的问题（🔗），和一个知乎提问（🔗），就没有任何其他相关的网页了，甚至连当年的提交记录都找不到。

既然如此，那就只能从这两个链接入手了。

  • Stack Overflow 的答主 Alex 写了一篇长文回答，但一开头就说「你需要理解 Permutation Cycle 的数学理论，才能理解这个算法」。于是我又回头恶补了一番组合数学，然而就算我大概知道 Permutation Cycle 是怎么一回事，对这个算法依然毫无头绪。（评论中也有人自称有 6 年抽象代数经验，但不认为这个算法与数学相关。）不过 Alex 的回答提供了一些有用的直觉，至少读完这个回答我大概理解 cycles 在算法执行过程中是如何变化的了。具体而言，cycles 的变化类似于「倒计时」，或者说「带借位的减法」，每次最后一位到 0 时，就会触发前面的一位减 1。然而我对indices 的变化依然云里雾里。
  • 知乎提问中，答主「杨个毛」提供了一个看起来很有说服力的回答（剧透：而且也的确如此）：「那个代码可以看成下列递归程序的强行非递归版」，指出了 cycles 是变进制数，并提供了一个原始递归版本。可惜的是，对于这个算法为什么可以输出正确结果依然没有解释（也有可能是我没有完全理解）。

自己来

已有的信息似乎不是很充分。看来我只能自己来了。在加了一堆 print 并在纸上手动模拟了多次这个算法之后，我认为我可能大概理解它的工作原理，并且可以证明其正确性了。下文将详述我的理解。

算法

起步

开始前，需要统一一下后文使用的记号：

  • n 代表输入 iterable 的长度
  • r 代表输出的排列元组的长度

并回顾我们先前阅读算法得到的理解：

  • 对输入的 iterable 会遍历其所有元素并放在 pool 中
  • 每次算法输出结果（yield），实际上只是取了 indices 列表的前 r 个 index，并输出 pool 中的对应元素。

我们将按照如下步骤理解这个算法：

  1. 理解 cycles 的变化
  2. 理解 indices 的变化，并尝试说明这个算法的正确性
  3. 尝试重新实现这个算法的「原始」递归版本

cycles

我们首先从 cycles 变量入手，理解它在这个算法中是如何变化的。这个阶段我们暂时先不考虑 indices。

可以先指定一些具体的输入，然后尝试加一些 print 语句。以 iterable="ABCD", r=2 作为输入，在 if 和 else 两个分支执行前后中都插入 print，可以得到如下结果：（其中中括号说明算法有输出 yield，大括号部分算法无输出）

[4,3] -> [4,2] -> [4,1] -> {4,0} -> {4,3} -> 
[3,3] -> [3,2] -> [3,1] -> {3,0} -> {3,3} -> 
[2,3] -> [2,2] -> [2,1] -> {2,0} -> {2,3} -> 
[1,3] -> [1,2] -> [1,1] -> {1,0} -> {1,3} -> {0,3} -> {4,3}

我们可以直观感受到，似乎 cycles 变量就像一个「倒计时」，或者说「带借位的减法」。

  • 一开始 cycles[0] 被初始化为 4，cycles[1] 被初始化为 3。
  • 之后的循环中，一般是 cycles[1] 不断被减 1。当 cycles[1] != 0 时，算法会产生一次输出。
  • 如果 cycles[1] == 0，会导致 cycles[0] （前一位）减 1，并将 cycles[1] 重设回其初始值 3。
  • 最后当 cycles[0] == 0 时，算法结束。

从这个具体的示例出发，我们可以这样理解 cycles 的变化：

  • 一开始 cycles 被初始化为 range(n, n-r, -1)，即 cycles[0]=n，cycles[1]=n-1，…，cycles[i]=n-i。
  • 之后的循环中，通常只有最后一个元素 cycles[r-1] 在不断递减。如果 cycles[r-1] 递减后值不为 0，则算法会产生一次输出。用我们之前提到的「倒计时」类比，可以将这种情况称之为 tick。
  • 如果 cycles 中的某个元素（如 cycles[i]）为 0，会导致其前面的元素被（cycles[i-1]）减 1，并将这个元素（cycles[i]）重设回其初始值（n-i）。这一行为类似于倒计时中秒为 0 时会导致分减 1，并将秒重设回 0。继续用「倒计时」类比，可以将这种情况称之为 reset。

有了这一直观感受，就可以为 cycles 找出一个可能的解释（「物理含义」）了。我认为，cycles 代表的是 「每个位置上剩余的可用选择数」 。如果将 cycles 视作一个变进制数，则 cycles 也代表 「总体剩余还没有输出的排列数」 。理由如下：

  • 一开始 cycles 被初始化为 range(n, n-r, -1)，而可以计算出对给定的 n, r 所有的排列有 P(n,r) = n*(n-1)*...*(n-r-1) 种。
  • 每次 tick，算法生成一个排列，消耗一个选择，cycles[i] 也减 1
  • 每次 reset，实际上就是在 cycles 这个变进制数上的借位减法
  • 最后在 cycles 上首位为 0 时算法结束，代表所有排列的选择都已经被消耗（输出）了，已经没有更多的排列了。

其实 cycles 的变化，无论是 Stack Overflow 上的回答，还是知乎上的回答，都有相对详尽的描述。在此我只是尝试以自己的语言重述了一次而已。但接下来对 indices 的理解就大部分是我自己的了。

indices

现在我们来看看 indices 是如何变化的。和之前对 cycles 的探索一样，我们也先从一个具体的例子开始：iterable="ABCDE",r=3，并关注一个子问题：前 3 个输出（ABC, ABD, ABE）是如何产生的。为便于展示，这里我直接使用具体元素（字母）代替 index。加了一些 print 后，我们可以得到如下的变化过程。

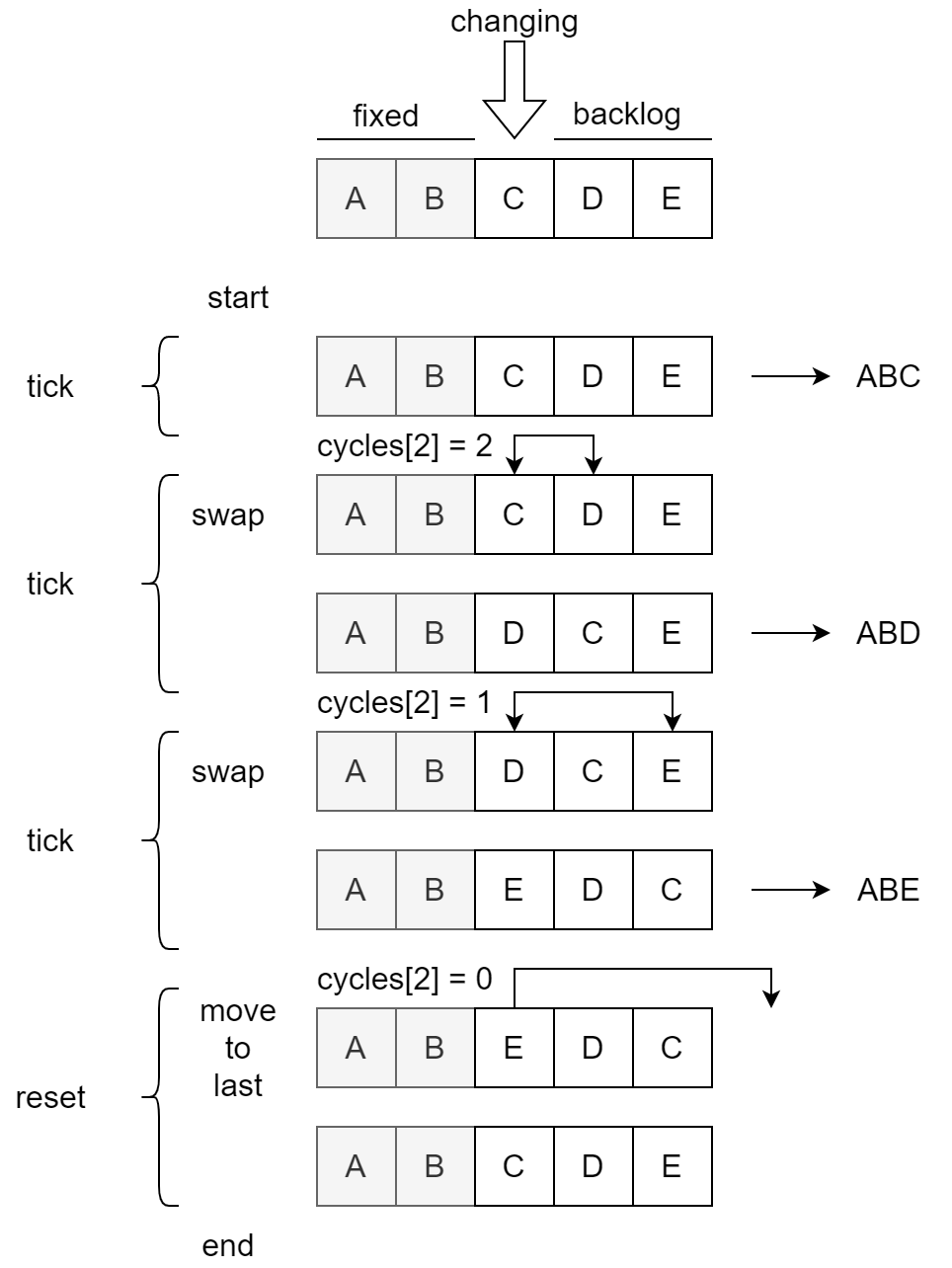
py_permutation

这个图稍微有些复杂。以下是进一步解释。

  • 图的阅读顺序是从上至下，按照时间顺序展示了indices 列表的变化。左侧为各阶段具体行为的标注，右侧为算法输出。
  • 这里选择展示前 3 次输出（即 i=2），对应 cycles[2] 从 3 到 0 的过程。别忘了每次进入循环前 cycles[2] 会被递减。
  • 为方便描述，我们可以把 indices 列表拆成 3 个部分：
    • fixed：indices[0:1]，在执行时不会变化
    • changing：indices[2]，这是在不断被交换的元素，和 fixed 一起组成了算法输出（indices[0:2]）
    • backlog：indices[3:4]，这里存放着已经被使用的元素和还未被使用的元素
  • 在每个 tick 中，changing 位置上的元素和 backlog 中的一个元素交换（swap），并触发一次输出。可以注意到，交换前后 backlog 中元素依然维持其相对顺序。
    • ABC{DE} -> ABD{CE} -> ABE{CD}
    • 注：这里将算法开始时的首次输出也视作一个 tick，因为进入循环前依然触发了递减，消耗了一个可能性。
    • 相关代码：indices[i], indices[-j] = indices[-j], indices[i]
  • 算法结束前，一共触发了 3 次输出。这已经穷尽了固定前缀为 AB，最后一个可选项为 C, D, E 的排列。
  • 在最后 reset 时，changing 位置上的元素被移到了 backlog 后（move_to_last）。这一步完成后，changing + backlog 这个子列表（indices[2:4]）恢复了和算法开始时一样的顺序。
    • AB{E}CD -> ABCD{E}
    • 相关代码：indices[i:] = indices[i+1:] + indices[i:i+1]

可以发现，这部分执行过程，恰好满足了回溯算法的正确性要求：

  • 分步解决一个问题，每步中固定之前步骤的选择不变
  • 算法执行中，遍历当前步的所有可能性
  • 算法执行后，取消当前步的计算，退回上一步，选择下一个可选项

虽然图中仅描述了一个子问题（i=2，或者说i=r-1），但不难发现对于其他的 i∈[0, r-1] 这一讨论都是成立的。这也（不严格地）说明了这一算法的确可以遍历所有的可能排列。输出顺序为字典序，则是因为每个 tick 中交换元素时都维护了 backlog 中的相对顺序。

这部分讨论有些复杂，如果不太理解（或者不完全信服）的话，可以自己多加点 print ，或者手动在纸上执行感受一下。

重新实现

现在我们已经了解了这个算法的原理，重新实现其原始递归版本也就不难了。

  • 递归调用时，需要一个参数指定当前修改的元素（changing）的 index
  • 在每一层调用中，交换 changing 和 backlog 中的所有项，并在每次交换（做出选择）后触发下一层
  • 如果 backlog 中的所有可选项都已经被选择（消耗）了，就把当前的 changing 移到 backlog 后，以撤销这一层的选择

以下是一个可能的 Python 重新实现。

## a reimplementation of `itertools.permutation`

# helpers
def swap(list, i, j):
    list[i], list[j] = list[j], list[i]

def move_to_last(list, i):
    list[i:] = list[i+1:] + [list[i]]

def print_first_n_element(list, n):
    print("".join(list[:n]))

# backtracking dfs
def permutations(list, r, changing_index):
    if changing_index == r:
        # we've reached the deepest level
        print_first_n_element(list, r)
        return
    
    # a pseudo `tick`
    # process initial permutation
    # which is just doing nothing (using the initial value)
    permutations(list, r, changing_index + 1)

    # note: initial permutaion has been outputed, thus the minus 1
    remaining_choices = len(list) - 1 - changing_index
    # for (i=1;i<=remaining_choices;i++)
    for i in range(1, remaining_choices+1):
        # `tick` phases
        
        # make one swap
        swap_idx = changing_index + i
        swap(list, changing_index, swap_idx)
        # finished one move at current level, now go deeper
        permutations(list, r, changing_index + 1)
    
    # `reset` phase
    move_to_last(list, changing_index)

# wrapper
def permutations_wrapper(list, r):
    permutations(list, r, 0)

# main
if __name__ == "__main__":
    my_list = ["A", "B", "C", "D"]
    permutations_wrapper(my_list, 2)

递归转循环优化

出于性能和安全（防止爆栈）的考量，我们会想将这个算法的递归版本转换成循环版本。这需要我们用栈手动维护每一层递归的相关状态，包括递归中的变量和下一次执行的开始位置。幸运的是，对这个算法而言，我们需要维护的状态并不多。

  • r 是已知且固定的，即栈的最大深度为 r，因此可以用一个固定大小的列表来表示栈中（每一层递归）的状态。

  • changing_idx 是每层递归的输入，代表当前层变化的元素。changing_idx 可以从栈的深度计算出来，栈底为 0，再上一层为 1… 因此实际上不需要维护。

  • i 或 swap_idx 为下一次交换的目标元素 index。这无法从栈本身的信息计算得到，需要我们维护。

  • 进入或重新回到当前层递归的开始位置，可以用 i 或 swap_idx 推算得到：如果还有剩余可选项，则跳转到 tick；反之跳转到 reset

基于上文分析，可以发现我们需要维护的栈有两个特点：

  • 长度固定为 r
  • 每个元素上维护下一次交换的目标元素 index

回头看看，这实际上就是 cycles。在「剩余可能数」的身份之外，cycles 也承担起了维护递归状态的职责。而作者巧妙利用了 Python 列表索引可以为负数从后往前的特性，统一了 cycles 的两面。

至此，我们完成了对这一算法的分析。🎉

相关链接

最后修改 2022-05-10